Clustering is hard, except when it's not

18 Nov 2015

The previous two posts (part 1, part 2) on clustering have been somewhat depressing and pessimistic. However, the reality is that scientists use simple clustering heuristics all the time, and often find interpretable results. What gives? Is the theoretical hardness of clustering flawed? Or have we just been deluding ourselves? Have we been fooled into believing results that are in some sense fundamentally flawed?

This post will explore a more optimistic possibility, which has been referred to as the “Clustering is Only Difficult When It Does Not Matter” hypothesis. Proponents argue that, while we can construct worst-case scenarios that cause algorithms to fail, clustering techniques work very well in practice because real-world datasets often have characteristic structure that more-or-less guarantees the success of these algorithms. Put differently, Daniely et al. (2012) say that “clustering is easy, otherwise it is pointless” — whenever clustering fails, it is probably because the data in question were not amenable to clustering in the first place.

Notation

In this post, we are going to view clustering as an optimization problem.

Let $\mathcal{C}$ denote a clustering (or partition) of a dataset into $k$ clusters.^[1]
Let $F(\mathcal{C})$ be the loss function (a.k.a objective function) that computes a “cost” or “badness” for any clustering.
Our goal is to find the best or optimal clustering (i.e. the one with the lowest value of $F$). We call the optimal clustering $C_{opt}$ , and the lowest/best value of the objective function $F_{opt}$.

\[\mathcal{C}_{\text{opt}} = \arg \min_{\mathcal{C}_i} F(\mathcal{C}_i)\] \[F_{\text{opt}} = \min_{\mathcal{C}_i} F(\mathcal{C}_i)\]

Example: $k$-means clustering results from choosing $F$ to be the sum-of-squared residuals between each datapoint $\mathbf{x}_j$ and the centroid ($\bar{\mathbf{x}}$) of the cluster it belongs to:

\[F(\mathcal{C}) = \sum_{i=1}^k \sum_{\mathbf{x}_j \in \mathcal{K}_i} \big\Vert \bar{\mathbf{x}}_i - \mathbf{x}_j \big\Vert^2_2\]

Example: $k$-medians clustering results from choosing $F$ to be the sum of the absolute residuals between each datapoint $\mathbf{x}_j$ and the mediod ($\tilde{\mathbf{x}}$) of the cluster it belongs to:

\[F(\mathcal{C}) = \sum_{i=1}^k \sum_{\mathbf{x}_j \in \mathcal{K}_i} \big \vert \tilde{\mathbf{x}}_i - \mathbf{x}_j \big \vert\]

For the purposes of this post, you can assume we’re using either of the above objective functions.^[2] Throughout this post, we assume that the number of clusters, $k$, is known a priori — analysis becomes very difficult otherwise.

Intuition behind easy vs. hard clustering

It is easy to construct datasets where it takes a very long time to find $\mathcal{C}_{\text{opt}}$. Consider the (schematic) dataset below. The data form an amorphous blob of points that are not easily separated into two clusters.

$Datapoints are shown as open circles, with color representing cluster assignment and x's denoting cluster centers. Two clusterings, $\mathcal{C}_1$ (left) and $\mathcal{C}_2$ (middle) are shown that have a similar loss. There are many local minima in the objective function (right). Disclaimer: schematic, not real data.$

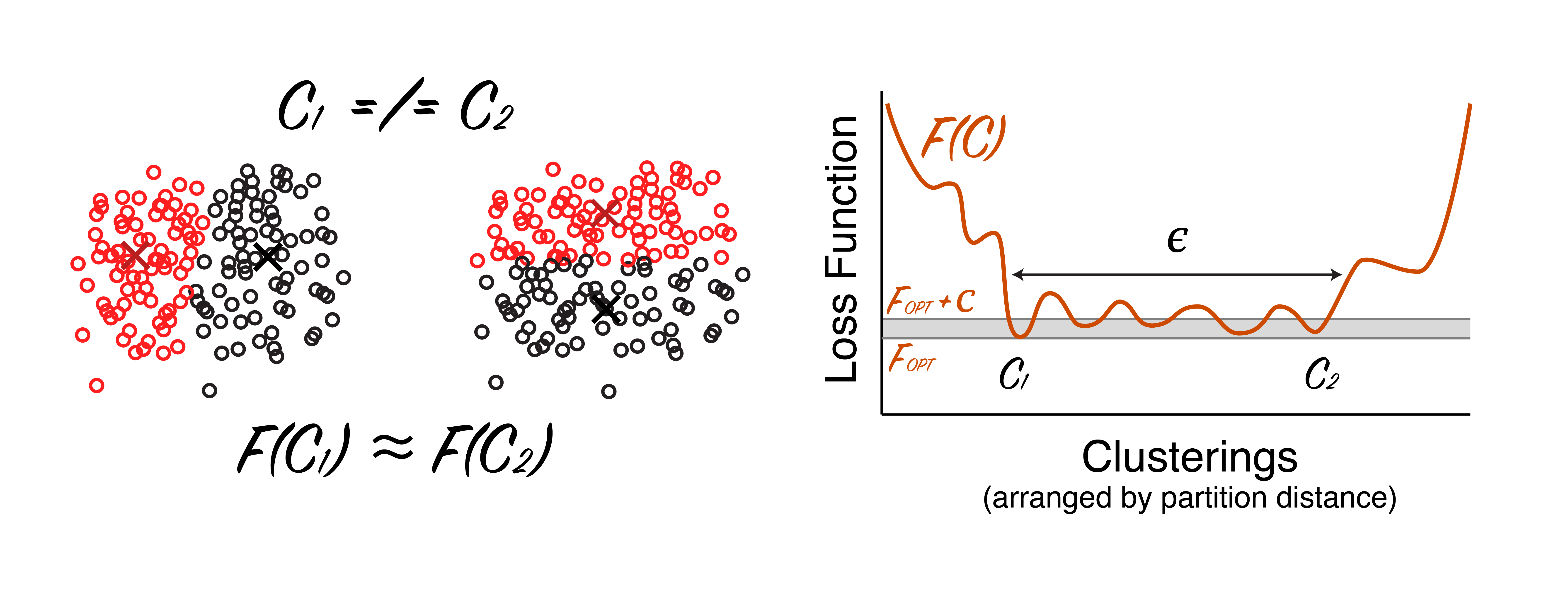A dataset not amenable to clustering. Datapoints are shown as open circles, with color representing cluster assignment and x's denoting cluster centers. Two clusterings, $\mathcal{C}_1$ (left) and $\mathcal{C}_2$ (middle) are shown that have a similar loss. There are many local minima in the objective function (right). Disclaimer: schematic, not real data.

In the above dataset we can find many clusterings that are nearly equivalent in terms of the loss function (e.g. $\mathcal{C}_1$ and $\mathcal{C}_2$ in the figure). Thus, if we want to be sure to find the very best clustering, we need to essentially do a brute force search.^[3] The “Clustering is Only Difficult When It Does Not Matter” hypothesis (and common sense) would tell us that it is stupid to do a cluster analysis on this dataset — there simply aren’t any clusters to be found!

Now compare this to a case where there are, in fact, two clearly separated clusters. In this case, there is really only one clustering that passes the “common sense” test. Assuming we pick a reasonable loss function, there should also be a very obvious global solution (unlike the first example):

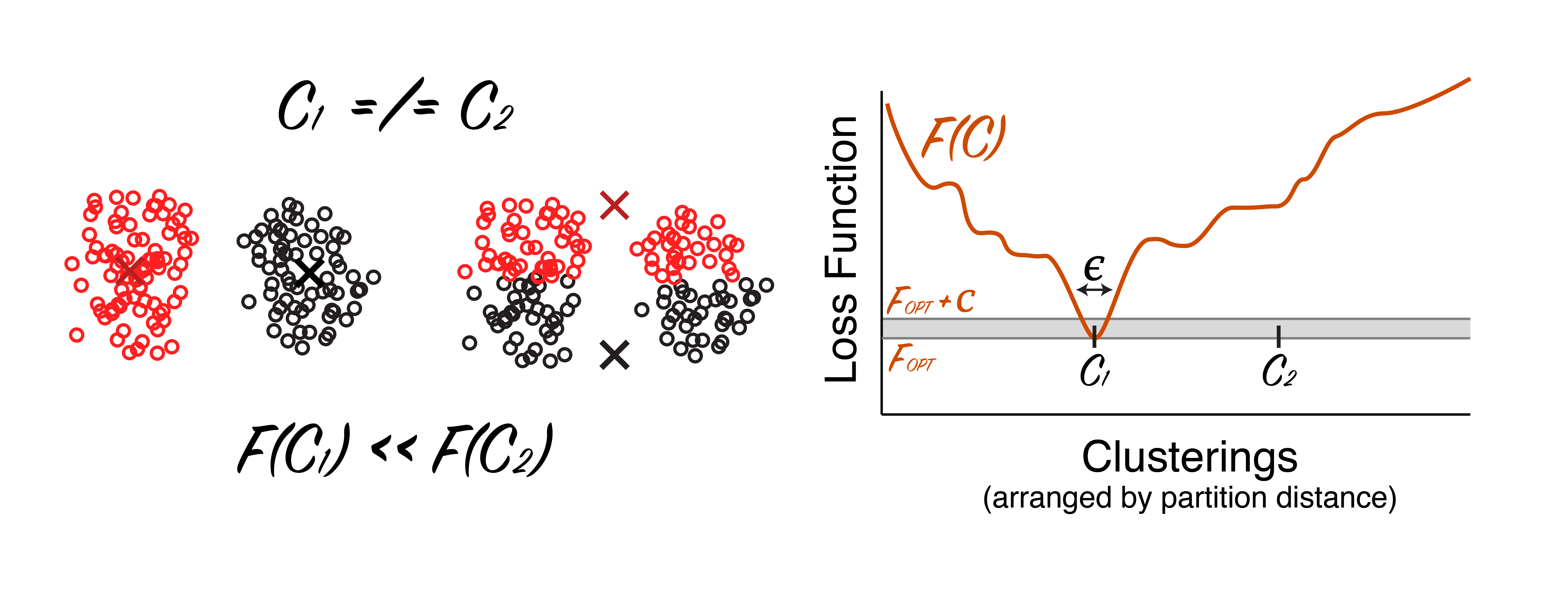As before, two clusterings are shown. The clustering on the <i>left</i> is much better in terms of the loss function than the clustering shown in the <i>middle</i>. <b><i>Disclaimer: schematic, not real data.</i></b>

A dataset that is easily clustered. As before, two clusterings are shown. The clustering on the left is much better in terms of the loss function than the clustering shown in the middle. Disclaimer: schematic, not real data.

Intuitively, it should be easier to find the solution for this second dataset: there is clear winner for the clustering, so there is an obvious global minimum, with few local minima. Remember, in the first dataset, there were multiple local minima that were nearly as good as the global minimum.

Provably “easy” clustering situations

We would like to formalize the intuition outlined in the previous section to develop efficient and accurate clustering algorithms. To do this we introduce the concept of approximation stability, which characterizes how “nice” the error landscape of the optimization problem is. In the schematic figures, the first difficult-to-cluster example is unstable, while the second easy-to-cluster example is stable. The ultimate punchline is that sufficiently stable clustering problems are provably easy to solve.

Definition: $(c,\epsilon)$-approximation-stability.

A clustering problem is said to be $(c,\epsilon)$-stable when all clusterings, $\mathcal{C^\prime}$, that satisfy $F(\mathcal{C}^\prime) \leq c F_{opt}$ also satisfy $d(\mathcal{C}^\prime,\mathcal{C}_{\text{opt}}) < \epsilon$. Here, $0 < \epsilon \ll 1$, and $c > 1$, and $d(\cdot,\cdot)$ measures the fraction of differently assigned datapoints between two clusterings.

The more stable the clustering problem is, the larger $c$ and the smaller $\epsilon$ are allowed to be. For example, if $c = 1.1$ and $\epsilon = 0.02$, then a problem is $(c,\epsilon)$-stable if all clusterings within 10% of the optimal objective value, are no more than 2% different from the optimal clustering.

As cluster stability increases, two things happen:

The problem becomes easier to solve. Balcan et al. (2013) provide several algorithms that are guaranteed to find near-optimal clusterings if the clusters are large enough and the problem is stable enough.^[4] These algorithms are very efficient,^[5] easy to implement, and similar to classic clustering algorithms.
Cluster analysis becomes more sensible and interpretable. While not immediately obvious, it turns out that approximation stability (as well as similar concepts, like perturbation stability) correlates with our intuitive sense of clusterability: when the data contain well-separated and compact clusters, then the clustering optimization problem is likely stable. This is outlined in Lemma 3.1 by Balcan et al. (2013).

In short, research along these lines is beginning to provide rigorous support for the “Clustering is Only Difficult When It Does Not Matter” hypothesis. To see the proofs associated with this work in detail check out the course materials for this class on “Beyond Worst-Case Analysis”. A particularly relevant lecture is embedded below (the others are also online):

Caveats

Shai Ben-David recently published a brief commentary on the “Clustering is Only Difficult When It Does Not Matter” hypothesis alongside a more detailed paper.^[6] He argues that, while the above results (and others) are encouraging, current theory has only shown clustering to be easy when clusters are very, very obvious in the dataset. For example, Ben-David digs into the specific results of Balcan et al. (2013) and concludes that their (simple, efficient) algorithm indeed produces the correct solution as clustering becomes stable enough. However, “stable enough” in this case more or less means that the majority of points sit more than 20 times closer to their true cluster than to any other cluster. This seems like a very strong assumption, which won’t hold for many practical applications.

There are other caveats to briefly mention.

We have restricted our discussion to center-based clustering frameworks (e.g. $k$-means and $k$-medians). This excludes the possibility of clustering more complicated manifolds. However, I’m not sure how much this matters. It is easy to dream up toy, nonlinear datasets (e.g. the Swiss Roll) that cause center-based clustering to fail. Are real-world datasets this pathological? Ensemble clustering provides a nice way to cluster non-linear manifolds with center-based techniques. Thus, to address this concern, it would be interesting to extend the theoretical results covered in this post to ensemble-based algorithms.
Throughout this post we have assumed that the number of clusters is known beforehand. Estimating the number of clusters ($k$) is a well-known and generally unsolved problem.^[7] In practice, we typically run clustering algorithms for various choices of $k$, and compare results in a somewhat ad hoc manner. For clustering to truly be “easy”, we need simple, consistent, and accurate methods for estimating $k$. While there is some work on this issue (e.g., Tibshirani et al., 2001), most of it is constrained to the case of “well-separated” clusters.

A theoretical understanding of clustering algorithms is desperately needed, and despite substantial caveats, it seems that we are beginning to make progress. I find the theoretical analysis in this area to be quite interesting and worthy of further work. However, it may be overly optimistic to conclude the “Clustering is only difficult when it does not matter”. Given current results, it is probably safer to conclude that “Clustering is difficult, except when it isn’t”.

The essential flavor of this work is part of a growing literature on finding provably accurate and efficient algorithms to solve problems that were traditionally thought to be difficult (often NP-Hard) to solve. A well-known example in the machine learning community is nonnegative matrix factorization (NMF) under the “separability condition.” While NMF is NP-hard in general, work by Arora et al. (2012) showed that it could be solved in polynomial time under certain assumptions (which were typically satisfied or nearly satisfied, in practice). Further work by Nicolas Gilles on this problem is worthy of special mention.

While all of this may seem a bit tangential to the topic of clustering, it really isn’t. One of the reasons NMF is useful is that it produces a sparse representation of a dataset, which can be thought of as an approximate clustering, or soft clustering of a dataset (Park & Kim, 2008). In other words, the very recent and very exciting work on provable NMF algorithms raises the tantalizing possibility that these ideas will soon provide deep insight into clustering.

Footnotes

[1] Explicitly, $\mathcal{C} = \{ \mathcal{K}_1,\mathcal{K}_2,…,\mathcal{K}_k\}$, where each $\mathcal{K}_i$ is a set of datapoints, $\mathcal{K}_i = \{\mathbf{x}_1^{(i)},\mathbf{x}_2^{(i)},…\}$, where $\mathbf{x}_j^{(i)}$, is a datapoint (a vector) in cluster $i$, indexed by $j$.

[2] It is instructive to prove that the arithmetic mean (i.e. centroid) of a set of points minimizes the sum-of-squared residuals. Similarly, the median minimizes the sum-of-absolute residuals.

[3] Speaking loosely, the necessity of this brute-force search makes finding the solution to the k-means optimization problem NP-hard (Aloise et al., 2009). Note that there are simple and efficient algorithms that find local minima, given an initial guess. However, solving the problem (i.e. finding and certifying that you’ve found the global minimum) is NP-hard in the worst-case.

[4] What, exactly, does it mean for a clustering problem to be “stable enough”? This is a very critical question, that is revisited in the caveats section.

[5] They run in polynomial time. Again, clustering problems are NP-hard in the worst case; they (probably) take exponential time to solve (assuming P $\neq$ NP).

[6] I borrowed his phrase — the “Clustering is Only Difficult When It Does Not Matter” hypothesis — for this post, although it is also a title of a older paper from a different group.