Why is clustering hard?

Clustering is a fundamental exploratory data analysis tool used in many scientific domains. Yet, there is “distressingly little general theory” on how it works or how to apply it to your particular data. Highlighting the difficulty of clustering, Larry Wasserman has joked that “mixtures, like tequila, are inherently evil and should be avoided at all costs.” (Andrew Gelman is slightly less pessimistic.)

The next few posts will dig into why clustering is hard a problem. Here, I will just demonstrate a couple examples to build intuition. Some of this intuition can be put on more solid theoretical footing — in the next post I plan to dig into Jon Kleinberg’s paper which precisely defines an ideal clustering function, but then proves that no such function exists and that there are inevitable tradeoffs that must be made.

Some references on clustering

There is a lot of material written on this already, so rather than re-hash what’s out there I will just point you to some good resources.

• K-means clustering (Wikipedia, Visualization by @ChrisPolis, Visualization by TECH-NI blog).

• Hierarchical/agglomerative clustering works by starting with each datapoint in its own cluster and fusing the nearest clusters together repeatedly (Wikipedia, Youtube #1, Youtube #2).

  • Single-linkage clustering is a particularly popular and well-characterized form of hierarchical clustering. Briefly, single-linkage begins by initializing each point as its own cluster, and then repeatedly combining the two closest clusters (as measured by their closest points of approach) until the desired number of clusters is achieved.

• Bayesian/probabilistic methods include finite mixture models and infinite mixture models. The connection between these methods and k-means is well-known (see, e.g., the textbooks of David MacKay and Kevin Murphy). I recommend Kulis & Jordan (2012) as a good paper to read on this connection.

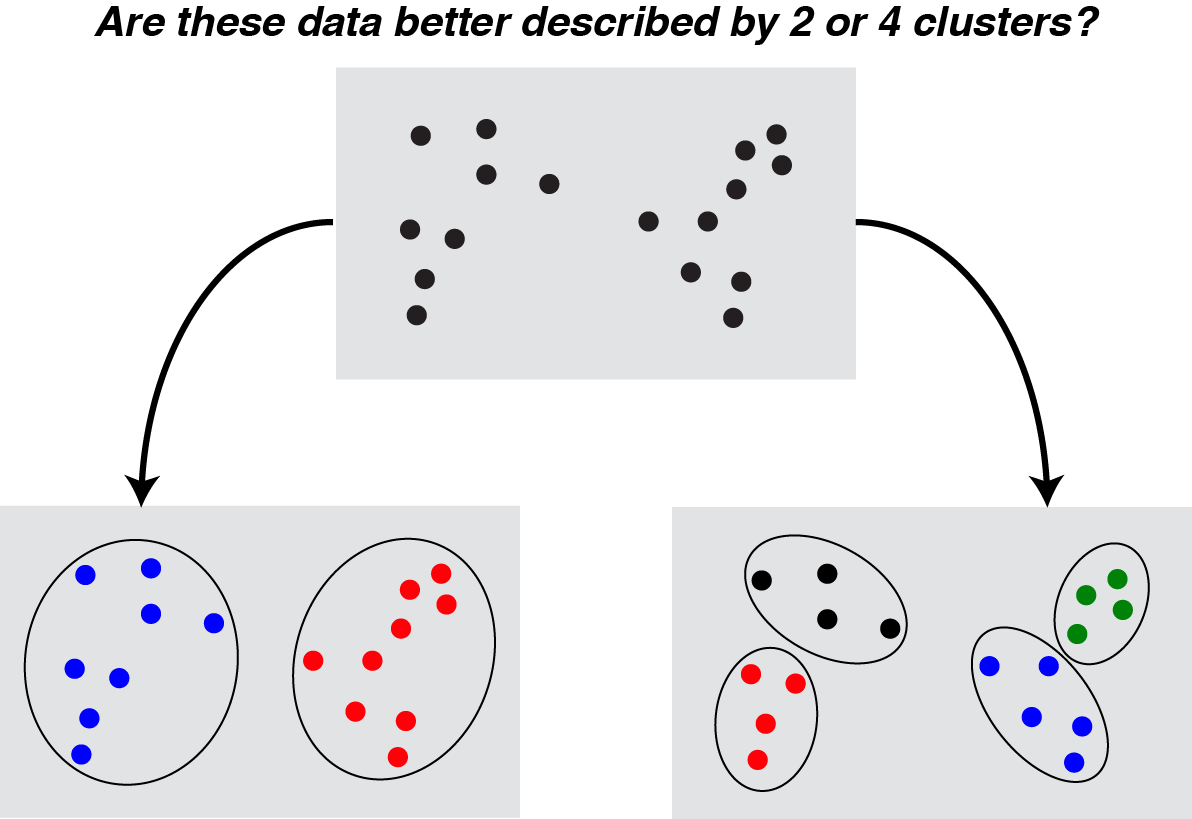
It is difficult to determine the number of clusters in a dataset

This has to be the most widely understood problem with clustering, and there is an entire Wikipedia article devoted to it. In most real-world datasets, there is no “true” number of clusters (though some numbers feel better than others), and that the same dataset is appropriately viewed at various levels of granularity depending on analysis goals.

While this problem cannot be “solved” definitively, there are some nice ways of dealing with it. Hierarchical/agglomerative clustering approaches provide cluster assignments for all possible number of clusters, allowing the analyst or reader to view the data across different levels of granularity. Other papers (see Chi & Lange, 2014, and refs. therein) have focused on convex clustering techniques. These fuse cluster centroids together in a continuous manner along a regularization path, exposing a similar hierarchical structure to agglomerative clustering, but with a k-means-like objective function. These hierarchical methods are nice because they enable exploratory analysis across multiple levels

There are also Bayesian approaches such as Dirichlet Process Mixture Models that directly estimate the number of clusters (alongside an estimate of uncertainty). However, this approach is by no means a panacea — other hyperparameters must still be tuned in these models, and they do not always estimate the number of clusters accurately (Miller & Harrison, 2013).

(Edit: in a later post I describe cross-validation approaches for estimating the number of clusters in a k-means model. This same approach can be applied to choose the number of model components in PCA and other matrix factorization models.)

It is difficult to cluster outliers (even if they form a common group)

David Robinson has a nice post on the shortcomings of k-means clustering, which is a quick and easy read. The following example he provides is particularly compelling:

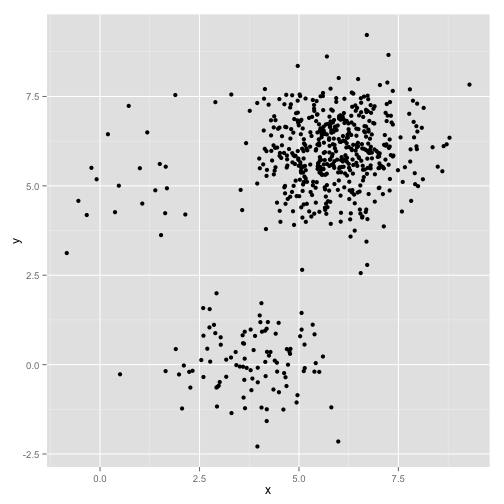Raw Data. Three spherical clusters with variable numbers of elements/points.

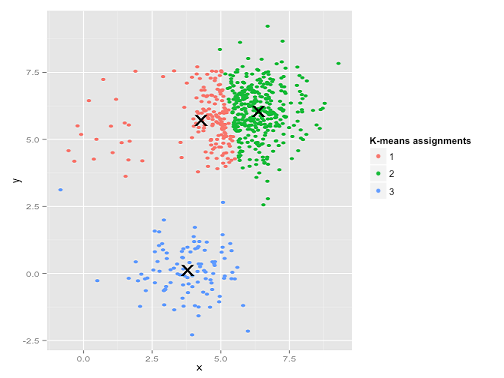
The human eye can pretty easily separate these data into three groups, but the k-means algorithm fails pretty hard:

Rather than assigning the points in the upper left corner to their own cluster, the algorithm breaks the largest cluster (in the upper right) into two clusters. In other words it tolerates a few large errors (upper left) in order to decrease the errors where data is particularly dense (upper right). This likely doesn’t align with our analysis, but it is completely reasonable from the perspective of the algorithm.

It is difficult to cluster non-spherical, overlapping data

A final, related problem arises from the shape of the data clusters. Every clustering algorithm makes structural assumptions about the dataset that need to be considered. For example, k-means works by minimizing the total sum-of-squared distance to the cluster centroids. This can produce undesirable results when the clusters are elongated in certain directions — particularly when the between-cluster distance is smaller than the maximum within-cluster distance. Single-linkage clustering, in contrast, can perform well in these cases, since points are clustered together based on their nearest neighbor, which facilitates clustering along ‘paths’ in the dataset.

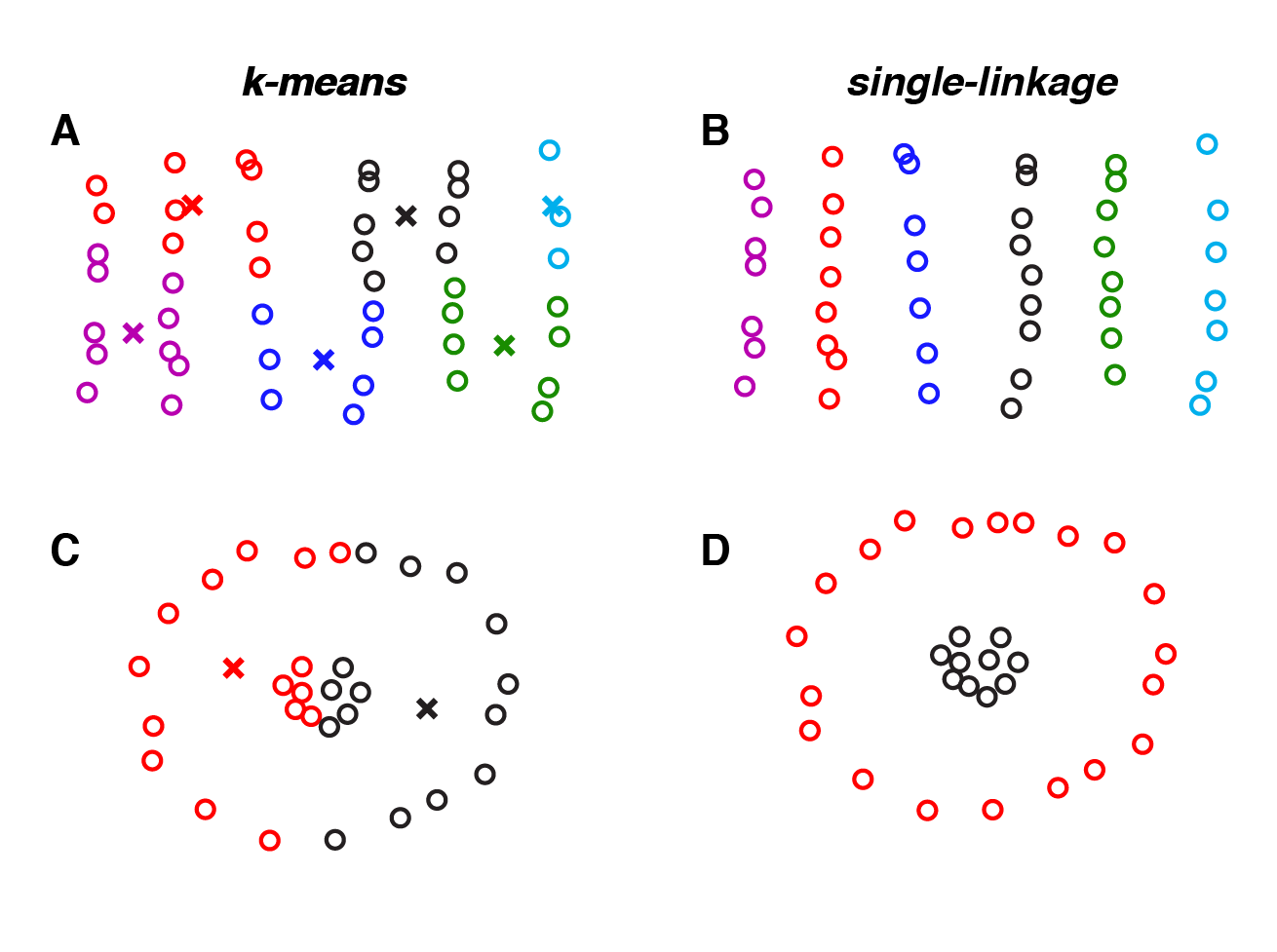Datasets where single-linkage outperforms k-means. If your dataset contains long paths, then single-linkage clustering (panels B and D) will typically perform better than k-means (panels A and C).

However, there is no free lunch. Single-linkage clustering is more sensitive to noise, because each clustering assignment is based on a single pair of datapoints (the pair with minimal distance). This can cause paths to form between overlapping clouds of points. In contrast, k-means uses a more global calculation — minimizing the distance to the nearest centroid summed over all points. As a result, k-means typically does a better job of identifying partially overlapping clusters.

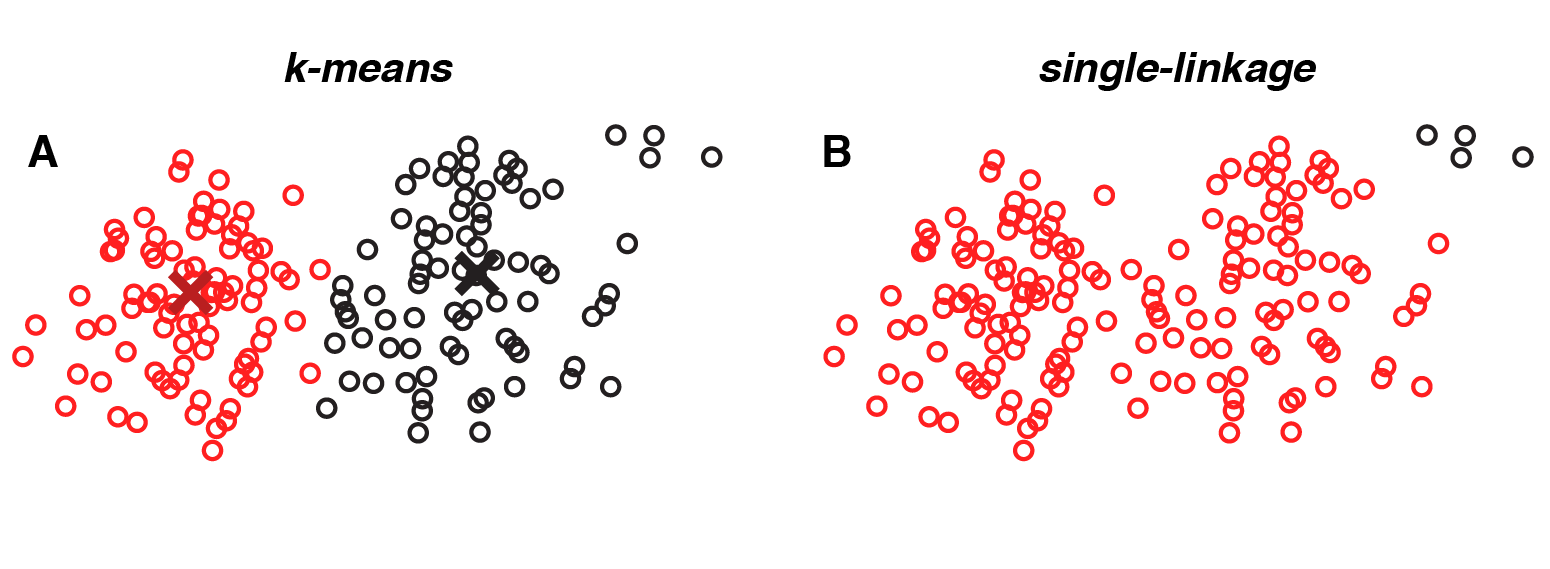A dataset where k-means outperforms single-linkage. Single-linkage clustering tends to erroneously fuse together overlapping groups of points (red dots); small groups of outliers (black dots) are clustered together based on their small pairwise distances.

The above figures were schematically reproduced from these lecture notes from a statistics course at Carnegie Mellon.

Are there solutions these problems?

This post was meant to highlight the inherent difficulty of clustering rather than propose solutions to these issues. It may therefore come off as a bit pessimistic. There are many heuristics that can help overcome the above issues, but I think it is important to emphasize that these are only heuristics, not guarantees. While many of biologists treat k-means as an “off the shelf” clustering algorithm, we need to be at least a little careful when we do this.