Is clustering mathematically impossible?

01 Oct 2015

In the previous post, we saw intuitive reasons why clustering is a hard,^[1] and maybe even ill-defined, problem. In practice, we are often stuck using heuristics that can sometimes perform quite badly when their assumptions are violated (see No free lunch theorem). Is there a mathematical way of expressing all of these difficulties? This post will cover some theoretical results of Kleinberg (2002) related to this question.

Notation. Suppose we have a set of $N$ datapoints $x^{(1)}, x^{(2)}, …, x^{(N)}$. A clustering function produces a partition (i.e. a set of clusters), based on the pairwise distances between datapoints. The distance between two points $x^{(i)}$ and $x^{(j)}$ is given by $d(x^{(i)},x^{(j)})$, where $d$ is the distance function. We could choose different ways to measure distance,^[2] for simplicity you can imagine we are using Euclidean distance, $\sqrt{ (x^{(i)}-x^{(j)}) \cdot (x^{(i)}-x^{(j)})}$.

An axiomatic approach to clustering

There are many possible clustering functions we could come up with. Some are stupid — randomly split the data into two groups — and others are useful in practice. We would like to precisely define what it means for a clustering function to be “useful in practice.”

Kleinberg (2002) proposed that the ideal clustering function would achieve three properties: scale-invariance, consistency, richness. The idea is that these principles should align with your intuitive notion of what a “good clustering function” is:

1. Scale-invariance: An ideal clustering function does not change its result when the data are scaled equally in all directions.

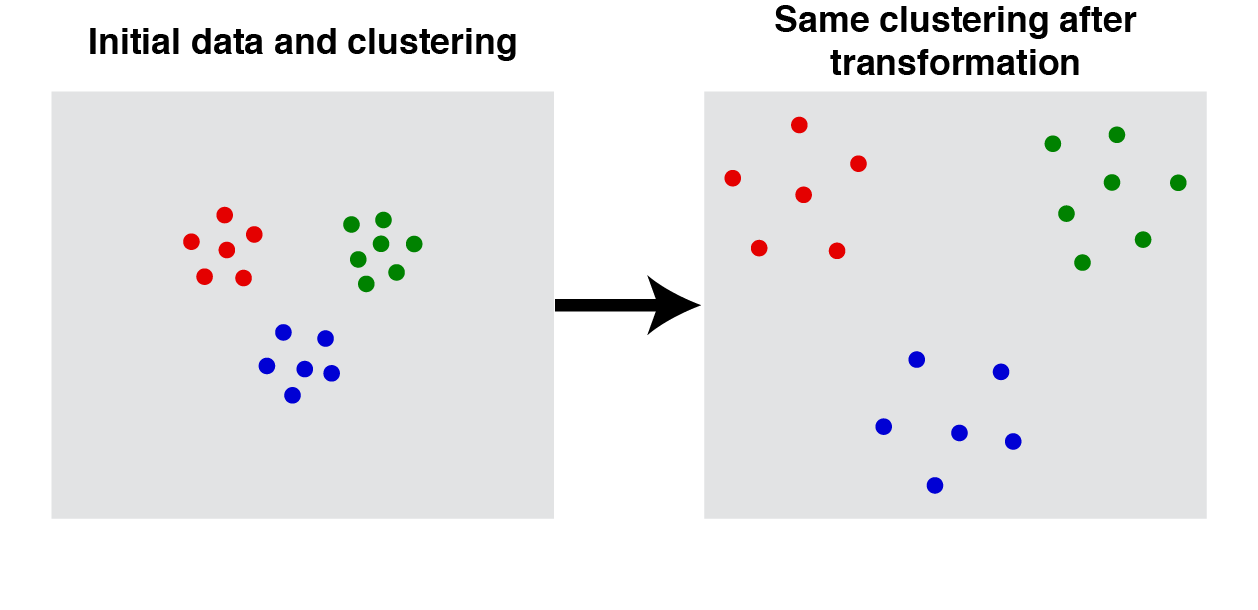$For any scalar $\alpha > 0$ the clustering function $f$ produces same result when the distances, $d$, between all datapoints are multiplied: $f(d) = f(\alpha \cdot d)$.$

Scale-invariance. For any scalar $\alpha > 0$ the clustering function $f$ produces same result when the distances, $d$, between all datapoints are multiplied: $f(d) = f(\alpha \cdot d)$.

2. Consistency: If we stretch the data so that the distances between clusters increases and/or the distances within clusters decreases, then the clustering shouldn’t change.

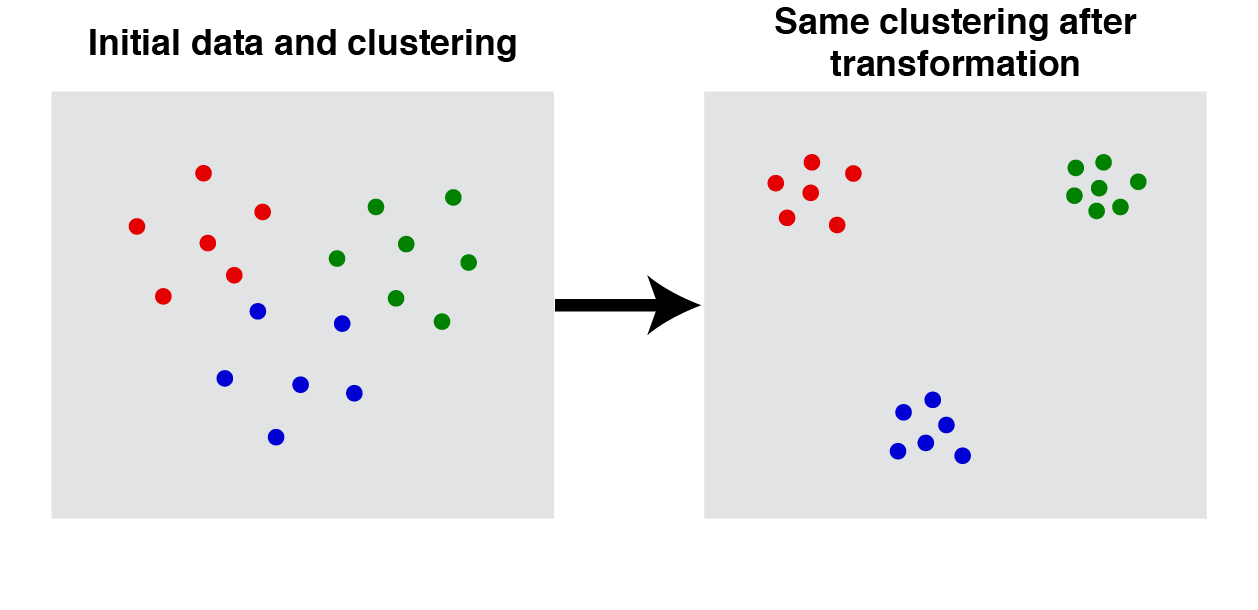$Let $d$ and $d^\prime$ be two distance functions. The clustering function produces a partition of points for the first distance function, $d$. If, for every pair $(i,j)$ belonging to the <i>same</i> cluster, $d(i,j) \geq d^\prime(i,j)$, and for every pair belonging to <i>different</i> clusters, $d(i,j) \leq d^\prime(i,j)$ then the clustering result shouldn't change: $f(d) = f(d^\prime)$$

Consistency. Let $d$ and $d^\prime$ be two distance functions. The clustering function produces a partition of points for the first distance function, $d$. If, for every pair $(i,j)$ belonging to the same cluster, $d(i,j) \geq d^\prime(i,j)$, and for every pair belonging to different clusters, $d(i,j) \leq d^\prime(i,j)$ then the clustering result shouldn't change: $f(d) = f(d^\prime)$

3. Richness: Suppose a dataset contains $N$ points, but we are not told anything about the distances between points. An ideal clustering function would be flexible enough to produce all possible partition/clusterings of this set. This means that the it automatically determines both the number and proportions of clusters in the dataset. This is shown schemetically below for a set of six datapoints:

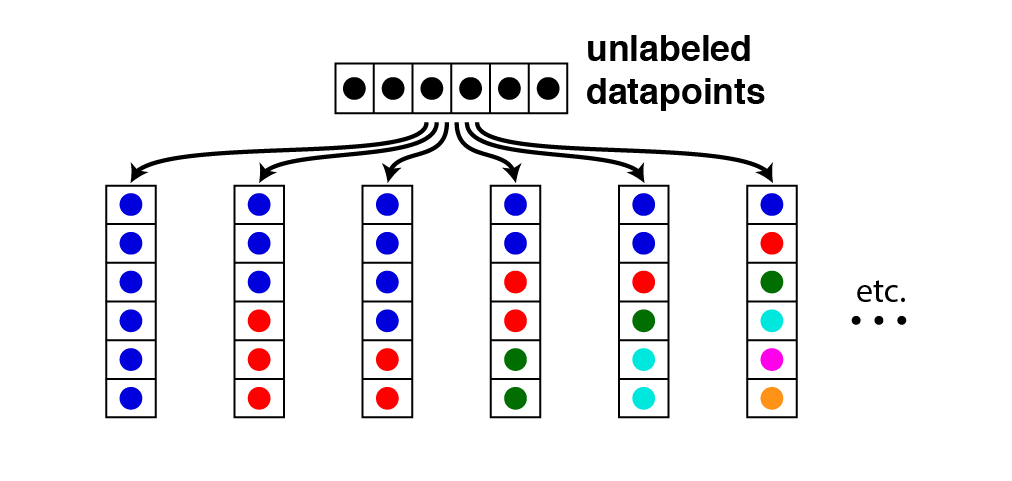$For a clustering function, $f$, richness implies that $\text{Range}(f)$ is equal to all possible partitions of a set of length $N$.$

Richness. For a clustering function, $f$, richness implies that $\text{Range}(f)$ is equal to all possible partitions of a set of length $N$.

Kleinberg’s Impossibility Theorem

Kleinberg’s paper is a bait-and-switch though. It turns out that no clustering function can satisfy all three axioms! ^[3] The proof in Kleinberg’s paper is a little terse — A simpler proof is given in Margareta Ackerman’s thesis, specifically Theorem 21. The intuition provided there is diagrammed below.

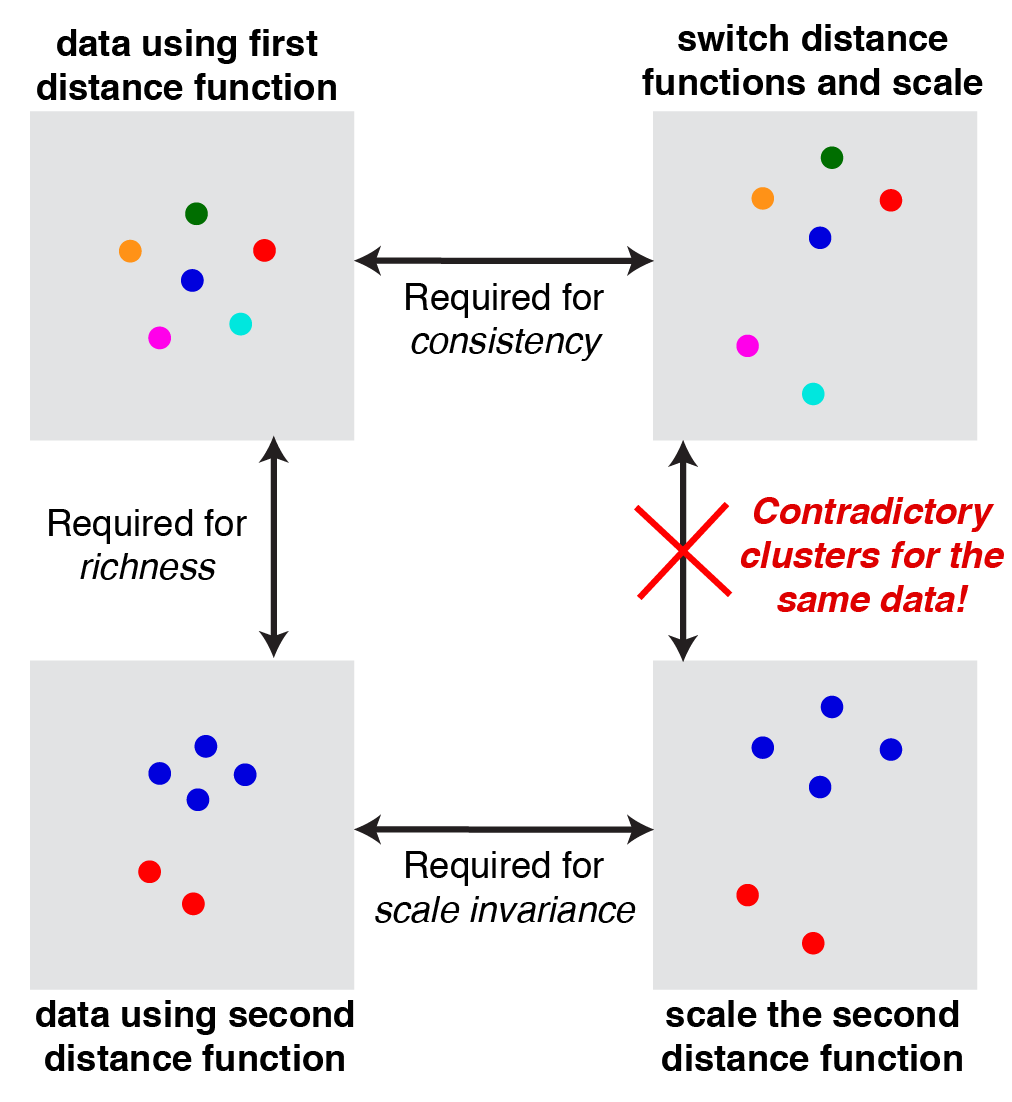$A consequence of the richness axiom is that we can define two different distance functions, $d_1$ (top left) and $d_2$ (bottom left), that respectively put all the data points into individual clusters and into some other clustering. Then we can define a third distance function $d_3$ (top and bottom right) that simply scales $d_2$ so that the minimum distance between points in $d_3$ space is larger than the maximum distance in $d_1$ space. Then, we arrive at a contradiction, since by consistency the clustering should be the same for the $d_1 \rightarrow d_3$ transformation, but also the same for the $d_2 \rightarrow d_3$ transformation.$

Intuition behind impossibility. A consequence of the richness axiom is that we can define two different distance functions, $d_1$ (top left) and $d_2$ (bottom left), that respectively put all the data points into individual clusters and into some other clustering. Then we can define a third distance function $d_3$ (top and bottom right) that simply scales $d_2$ so that the minimum distance between points in $d_3$ space is larger than the maximum distance in $d_1$ space. Then, we arrive at a contradiction, since by consistency the clustering should be the same for the $d_1 \rightarrow d_3$ transformation, but also the same for the $d_2 \rightarrow d_3$ transformation.

Clustering functions that satisfy two of the three axioms

The above explanation may still be a bit difficult to digest. Another perspective for understanding the impossibility theory is to examine clustering functions that come close to satisfying the three axioms.

Kleinberg mentions three variants of single-linkage clustering as an illustration. Single-linkage clustering starts by assigning each point to its own cluster, and then repeatedly fusing together the nearest clusters (where nearest is measured by our specified distance function). To complete the clustering function we need a stopping condition — something that tells us when to terminate and return the current set of clusters as our solution. Kleinberg outlines three different stopping conditions, each of which violates one of his three axioms, while satisfying the other two.

1. $k$-cluster stopping condition: Stop fusing clusters once we have $k$ clusters (where $k$ is some number provided beforehand, similar to the k-means algorithm).

This clearly violates the richness axiom. For example, if we choose $k=3$, then we could never return a result with 2 clusters, 4 clusters, etc. However, it satisfies scale-invariance and consistency. To check this, notice that the transformations in the above diagrams above do not change which $k$ clusters are nearest to each other. It is only once we start merging and dividing clusters that we get into trouble.

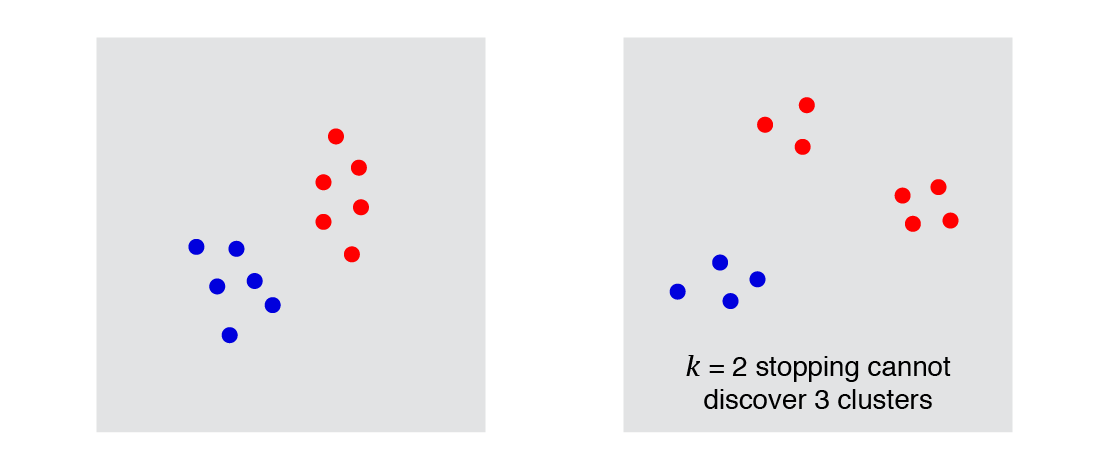$k$-cluster stopping does not satisfy richness

2. Distance-$r$ stopping condition: Stop when the nearest two clusters are farther than a pre-defined distance $r$.

This satisfies richness — we can place $N$ points to end up in $N$ clusters by having the minimum distance between any two points to be greater than $r$, we can place $N$ points to end up in one cluster by having the maximum distance be less than $r$, and we can generate all partitions between these extremes.

It also satisfies consistency. Shrinking the distances between points in a cluster keeps the maximum distance less than $r$ (our criterion for defining a cluster in the first place). Expanding the distances between points in different clusters keeps the minimum distance greater than $r$. Thus, the clusters remain the same.

However, scale-invariance is violated. If we multiply the data by a large enough number, then the $N$ points will be assigned $N$ different clusters (all points are more than distance $r$ from each other). If we multiply the data by a number close to zero, everything ends up in the same cluster.

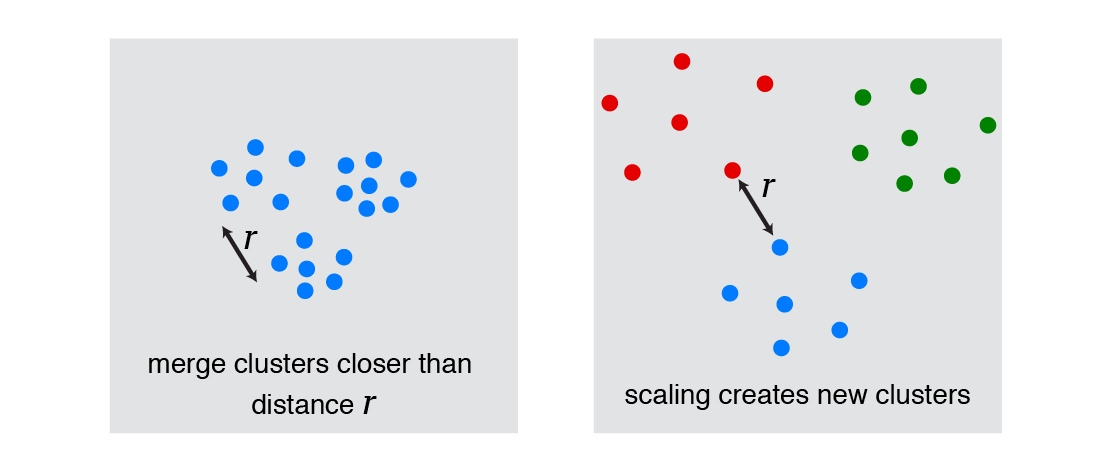distance-$r$ stopping does not satisfy scale-invariance

3. Scale-$\epsilon$ stopping condition: Stop when the nearest two clusters are farther than a fraction of the maximum distance between two points. This is like the distance-$r$ stopping condition, except we choose $r = \epsilon \cdot \Delta$, where $\Delta$ is the maximum distance between any two data points and $\epsilon$ is a number between 0 and 1.

By adapting $r$ to the scale of the data, this procedure now satisfies scale-invariance in addition to richness. However, it does not satisfy consistency. To see this, consider the following transformation of data, in which one cluster (the green one) is pulled much further away from the other two clusters. This increases the maximum distance between data points, leading us to merge the blue and red clusters into one:

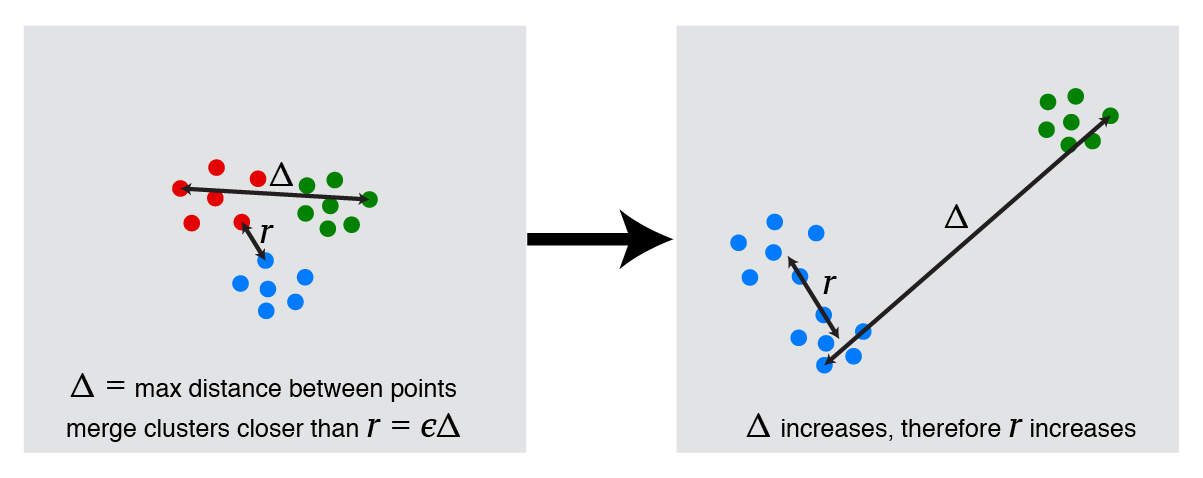scale-$\epsilon$ stopping does not satisfy consistency

Sidestepping impossibility and subsequent work

Kleinberg’s analysis outlines what we should not expect clustering algorithms to do for us. It is good not to have unrealistic expectations. But can we circumvent his impossibility theorem, and are his axioms even really desirable?

The consistency axiom is particularly suspect as illustrated below:

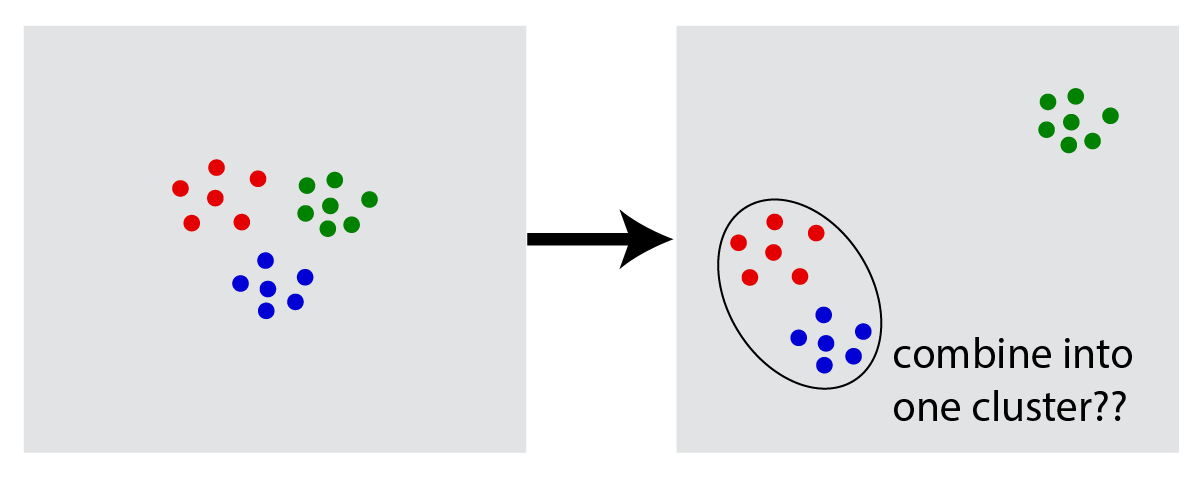Is consistency a desirable axiom?

The problem is that our intuitive sense of clustering would probably lead us to merge the two clusters in the lower left corner. This criticism is taken up in Margareta Ackerman’s thesis, which I hope to summarize in a future blog post.

Many clustering algorithms also ignore the richness axiom by specifying the number of clusters beforehand. For example, we can run $k$-means multiple times with different choices of $k$, allowing us to re-interpret the same dataset at different levels of granularity. Zadeh & Ben-David (2009) study a relaxation of the richness axiom, which they call $k$-richness — a desirable clustering function should produce all possible $k$-partitions of a datset (rather than all partitions).

Overall, Kleinberg’s axiomatic approach provides an interesting perspective on clustering, but his analysis serves more as a starting point, rather than a definitive theoretical characterization of clustering.

Footnotes

[1] I am using loose language when I say clustering is a “hard problem.” Similar to the previous post, we will be concerned with why clustering is hard on a conceptual/theoretical level. But it is also worth pointing out that clustering is hard on a computational level — it takes a long time to compute a provably optimal solution. For example, k-means is provably NP-hard for even k=2 clusters (Aloise et al., 2009). This is because cluster assignment is a discrete variable (a point either belongs to a cluster or does not); in many cases, discrete optimization problems are more difficult to solve than continuous problems because we can compute the derivatives of the objective function and thus take advantage of gradient-based methods. (However this doesn’t entirely account for the hardness.)

[2] Kleinberg (2002) only requires that the distance be nonnegative and symmetric, $d(x_i,x_j) = d(x_j,x_i)$, and not necessarily satisfy the triangle inequality. According to Wikipedia these are called semimetrics. There are many other exotic distance functions that fit within this space. For example, we can choose other vector norms $d(x,y) = ||x -y||$ or information theoretic quantities like Jensen-Shannon divergence.

[3] Interesting side note: the title of Kleinberg’s paper — An Impossibility Theorem for Clustering — is an homage to Kenneth Arrow’s impossibility theorem, which roughly states that there is no “fair” voting system in which voters rank three or more choices. As in Kleinberg’s approach, “fairness” is defined by three axioms, which cannot be simultaneously satisfied.